

Note that as we considered the first 10, 100 and 1,000 integers, the percentage of primes went from 40% to 25% to 16.8%. Among the first 1,000 integers, there are 168 primes, so π(1,000) = 168, and so on. Similarly, π(100) = 25, since 25 of the first 100 integers are prime. This value is called π( n), where π is the “prime counting function.” For example, π(10) = 4 since there are four primes less than or equal to 10 (2, 3, 5 and 7). The prime number theorem provides a way to approximate the number of primes less than or equal to a given number n.
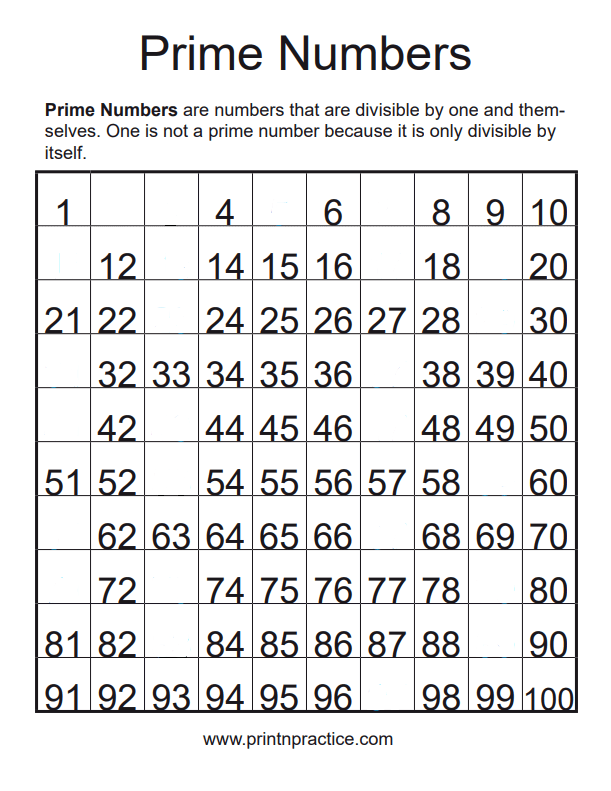
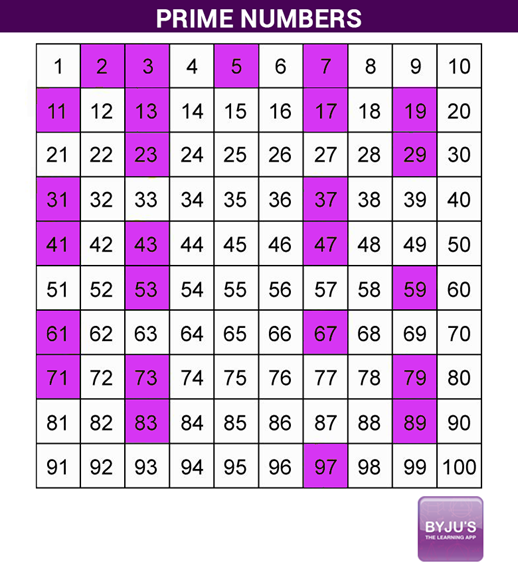
While mathematicians never know whether a proof would merit inclusion in The Book, two strong contenders are the first, independent proofs of the prime number theorem in 1896 by Jacques Hadamard and Charles-Jean de la Vallée Poussin. One favorite is the prime number theorem - a statement that describes the distribution of prime numbers, those whose only divisors are 1 and themselves. Erdős’ mandate hints at the motives of mathematicians who continue to search for new proofs of already proved theorems. The Book, which only exists in theory, contains the most elegant proofs of the most important theorems. “You don’t have to believe in God, but you have to believe in The Book,” the Hungarian mathematician Paul Erdős once said.


 0 kommentar(er)
0 kommentar(er)
